When I initially launched Bitcoin in 2009, I noted two ways of sending bitcoin [1]:
There are two ways to send money. If the recipient is online, you can enter their IP address and it will connect, get a new public key and send the transaction with comments. If the recipient is not online, it is possible to send to their Bitcoin address, which is a hash of their public key that they give you. They'll receive the transaction the next time they connect and get the block it's in. This method has the disadvantage that no comment information is sent, and a bit of privacy may be lost if the address is used multiple times, but it is a useful alternative if both users can't be online at the same time or the recipient can't receive incoming connections.
The addressing mechanism was not designed to be the only way of sending money to other users, which has been deployed very badly. I had explained that reusing public keys was not a good idea. Every single use of bitcoin should correspond to a new address. Even when a user is offline, the scenario should not be difficult. As an example, I shall endeavour to take the reader through one possible scenario that solves the problem very quickly and maintains a high level of security and privacy.
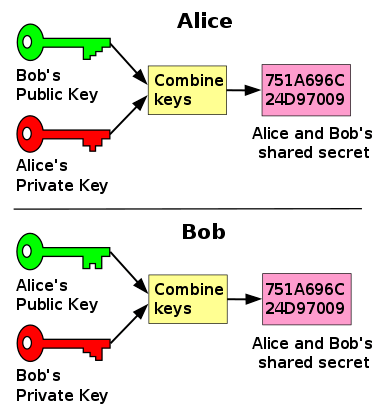
We will start with Alice, who is seeking to purchase goods from Bob. Bob has a website. Even if Bob didn't have a website, to send to an address owned by Bob, there must have been some way for Alice and Bob to exchange information in the past. Alice cannot merely send to a random address, without knowing information about Bob. So, we have defined that there must be some knowledge of what Bob's address is.
Rather than using the typical Bitcoin address, in a manner that does little to protect privacy, we will attribute a public key to Bob and Alice. Such a key could be certified using a certification authority (CA) or distributed using a web of trust. As long as it is known that Bob and Alice are attributed a particular key, Bob and Alice can remain pseudonymous and still engage. The communications between Bob and Alice, although publicly disseminated over the Bitcoin blockchain, will be completely private. We can define the following terms:
P_Alice Alice’s root public key P_Alice = s_A.G
C(P_Alice) A certified certificate of Alice's key [2]
S_A Alice's secret key
P_Bob Bob’s root public key P_Bob = s_B.G
C(P_Bob) A certified certificate of Bob's key [2]
S_B Bob's secret key
Bob can publish his certified public key on his website. Companies use public keys in SSL/TLS connections to websites, and Bob could even certify a domain. When connecting to websites, the keys do not change. But, because Bitcoin entails a public ledger that everyone can view, we don't want to keep using the same key. Bob must create an algorithm that allows another individual, such as Alice, to transact with him without using the same key multiple times.
Bob uses a standard protocol to disseminate information. Such protocols can be distributed on a website or use information in the same way protocols are defined on the Internet. Here, we will assume that Bob uses a simple algorithm that has been widely distributed and is used across many Bitcoin wallets in the future. For such an algorithm, several values are calculated. The calculation of addresses would be automated and simply require that Bob and Alice know each other's master public key.
S_AB = P_Alice x s_B = P_Bob x s_A
The secret, S_AB, would be calculated using your own secret key and the other party's public key. Only Alice and Bob know how to calculate S_AB. Such a simple protocol makes it possible to create a secure messaging format that never disseminates the exchanges between the original public-key holders on-chain. Using it would allow us to create an HMAC [3] of exchanged information such as a purchase order or invoice number.
Hm(i) = HMAC (S_AB, m)
m = Invoice(i)
The message (m) could be any value. It could be the hash of a document or anything else we wish to exchange. Here, we have used the invoice number "i". The Elliptic Curve Digital Signature Algorithm (ECDSA), the elliptic curve algorithm used in Bitcoin, has some interesting properties.

Both Bob and Alice can calculate a derivative address that will be associated with Bob. ECDSA has some additive properties that allow for the secure summation of keys. We can create a single-use, additive key function using the shared value Hm(i).
P(i) = Hm(i).G
The value G is the curve multiplier, that all parties know. Both Alice and Bob could calculate P(i) and know the secret if it was used. But, because of the additive nature of addressing, Alice can now create an offline subkey that Bob has never used but will be able to generate later.
P_Bob(i) = P(i) + P_Bob
The public key that has been derived, P_Bob(i), can easily be calculated by either Bob or Alice, but no other party can relate it to Bob or Alice, even though it is publicly available on the blockchain. And even though Alice can calculate Bob's new derivative public key that she is sending bitcoin to, she does not have Bob's private key s_B, which would be required to unlock the bitcoin and spend it. So, Alice knows where she has sent the transaction to, and can now inform Bob using email or any other methodology to exchange information offline.
Using the same existing methodology that is available and was created as the first payment template for Bitcoin, we can take the hash of the hash of Bob's public address key as follows:
Address(Bob_i) = Hash256(Hash256(Pub_Bob(i)))
This address function works and is formatted as the original addressing function in Bitcoin. Yet, the system allows Alice and Bob to create a series of addresses that change over time. For instance, Alice could update an invoice or other number and create an entirely new set of addressing schemes. The wallet software would take Bob's public key and a value such as an invoice number, which is all Alice would need to compute the output address for Bob.
With Alice's master public key and the invoice number, even if Bob is offline, he will receive funds from Alice. There is no way for a third party such as Charlie to attribute the payment address, Address(Bob_i), to either Bob or Alice using their public keys displayed through a certification authority (CA) or otherwise. Similarly, even after Bob has spent the bitcoin associated with the address, the public key, P_Bob(i), will not be publicly linked to the master key, allowing him to remain private.
Many possible protocols could be created on top of Bitcoin. The one described in today’s post is based on the original protocol and templates that existed in 2009, when I launched Bitcoin. When I say that addressing is being misused, I'm referring to the reuse of keys. The ability to calculate derivative keys and to automate the process existed when Bitcoin was launched. None of it entails a new technology. Yet, many new things are created using old technologies. Right now, the drive to make a system that acts outside of the controls of Bitcoin has led to many problems. When people stop trying to change the underlying protocol, you can start seeing how many things can be built. Innovation does not come about by changing foundations; it comes through building upon them.
References
1. Bitcoin v0.1 Alpha Release [Original Bitcoin website]. (2009, Mar 3). Wayback Machine. https://web.archive.org/web/20090303195936/http://bitcoin.org/
2. Russell, A. (2019, July 23). What Is a Certificate Authority (CA)?. SSL.com. https://www.ssl.com/faqs/what-is-a-certificate-authority/#:~:text=A%20certificate%20authority%20(CA)%2C,the%20issuance%20of%20electronic%20documents
3. HMAC. (2021, January 12). In Wikipedia. https://en.wikipedia.org/w/index.php?title=HMAC&oldid=999850157